Falling elements

Contexte
Le but de ce projet personnel est de refaire un des jeux de type "Falling-sand" que l'on peut retrouver en ligne.
Ces jeux laissent l'utilisateur interagir avec différents éléments, pouvant produire de nombreuses réactions entre eux.
Comme le jeu ne possède pas de but à proprement parler, on appelle ce genre "bac à sable", car il permet au joueur de faire tout ce qu'il souhaite, sans aucune contrainte.
Ce type de jeu se base généralement sur un moteur utilisant des "particules" ou "cellules" dans un tableau en deux dimensions.
Le plus connu de ce genre étant le Jeu de la vie de John Horton Conway.
On retrouve cependant des versions bien plus récentes et poussées comme avec le jeu Noita, sorti en 2019.
Pour réaliser ce projet j'utiliserai le langage C++ couplé à OpenGL pour la partie graphique.
Sommaire
- Afficher une grille avec OpenGL
- Concevoir les cellules et leurs caractéristiques
- Actualiser les cellules
- Créer différents comportements
- Conclusion
- Sources
Réalisation
Afficher une grille avec OpenGL
L'avantage de ne pas utiliser un moteur de jeu préfait comme dans de précédents projets avec Unity, est de pouvoir faire une application sur mesure.
Seul les éléments nécessaires au projet seront présents, ce qui permet d'améliorer la taille du projet ansi que ses performances.
En revanche, toutes les fonctionnalités préfaites pouvant se trouver dans un moteur sont à reprogrammer ce qui augmente le travail à fournir.
Comme ici le seul objectif est de pouvoir afficher des couleurs sur une grille, il est acceptable de se passer d'un moteur de jeu existant.
OpenGL utilise des triangles pour afficher des couleurs sur notre écran.
Il faut donc lui fournir les trois points qui constituent chaque triangle, ainsi que leurs couleurs.
On va alors parler de "vertex". Chaque vertex, va contenir une position ainsi qu'une couleur.
Une fois les vertex définies, il faut indiquer quels vertex relier entre eux en précisant leurs indices afin de former un carré.
Voici un schéma illustrant comment afficher un carré.
C'est en appliquant ce principe pour plusieurs carrés qu'il est possible de refaire une grille où chaque carré peut changer de couleur.

Cependant, plus le nombre d'éléments dans la grille est grand, plus l'affichage mettra du temps à s'effectuer.
Pour pallier à ce soucis, il est possible d'utiliser la technique du "batch rendering".
Au lieu d'afficher chaque triangle un par un, le batch rendering va regrouper un grand nombre de ces triangles pour les afficher tous en même temps.
Bien sûr, cette technique n'est pas magique est ne fonctionne pas pour une infinité de triangles.
Elle permet cependant de rendre fluide l'affichage d'une centaine de millier de carrés, ce qui est difficilement réalisable sans cette technique.
Actuellement les couleurs affichées par la grille sont définies à la main. La prochaine étape est de créer la base qui va permettre de donner vie à cette grille de couleurs.
Concevoir les cellules et leurs caractéristiques
Il est donc temps de créer ces fameux "éléments". Chaque élément possèdera un ensemble de règles leurs permettant permettant de reproduire un comportement désiré.
Commençons par définir de quoi seront composées ces cellules.
Etant donné que la grille vient d'être réalisée, il parait essentiel que chaque cellule possède une couleur.
Il est également primordial d'avoir une position. Cette position sera utile pour savoir où se situe la cellule dans la grille en deux dimensions.
Pour différencier les différents états de matières, les cellules possèderont un type correspondant à "solide", "liquid" ou "gazeux".
Viens, ensuite la question de comment définir ces fameux comportements ?
Une solution serait d'utiliser le système d'héritage du langage C++, afin de créer différents types de cellules (solides, liquides, gazeuses).
Et à partir de ces grands groupes, il serait ensuite possible de sous-diviser ces types pour créer des éléments de manière plus précise.
Par exemple dans les solides, d'avoir des cellules, roches, sable, terre, etc...
La deuxième solution se sert du principe de composition.
En programmation orientée objet, la composition est le fait d'avoir une instance d'une classe dans une autre.
Chaque cellules possèderaient alors un objet, correspondant à un des différents comportements programmé.
Dans l'optique de généraliser au maximum les cellules, il est préférable d'opter pour la composition.
Celles-ci devraient être définies par ce qui les composent, et non pas par une hiérarchisation entre différentes classes.
Cela permet d'avoir de nouveaux types de cellules, favorisant ainsi la création de comportements émergeant.
Il est à noter que les cellules ne possèdent pour l'instant que peu de caractéristiques, mais de nouvelles en seront rajoutées au fur et à mesure que le projet avance.
Pour utiliser son comportement, il faut qu'une cellule sache quelle méthode appeller et ce, quel que soit le comportement qu'elle possède.
Autrement dit, le nom de la méthode doit rester le même malgré ses différentes implémentations possibles.
Utiliser le système d'interface du langage C++ est donc très pratique pour créer différents types de comportements.
Une interface permet de désigner un ensemble de fonctionnalités sans implémentation.
Ces fonctionnalités seront uniquement définies par les classes dérivées.
Toutes les cellules doivent posséder un membre nommé IMovementBehavior.
La méthodeupdatepermet à chaque cellule d'utiliser sa fonction de mouvement implémentée par une classe héritant de IMovementBehavior.
Pour commencer à implémenter un premier comportement de déplacement, le sable est idéal car son fonctionnement est simple.
En grande quantité, le sable doit former des dunes.
Pour cela il doit non seulement subir l'effet de la gravité mais également celui du glissement lorsqu'il est en pente.
Ces conditions appliquées à notre grille en deux-dimensions se résument avec le schéma ci-contre.
Le mouvement directement sous lui (représenté par la flèche rouge) est testé avant ceux de côtés (représentées par les flèches vertes).
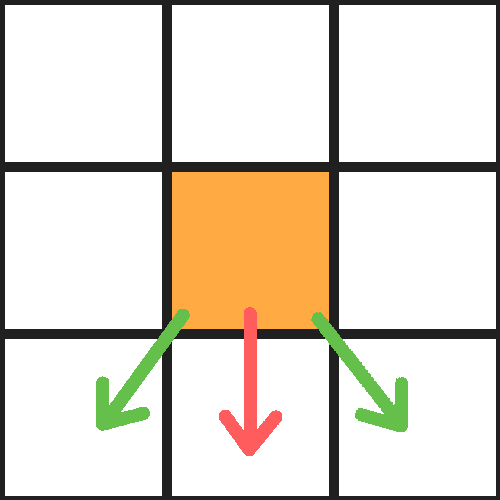
Pour que le comportement d'une cellule puisse modifier les informations de celle-ci (par exemple sa position),
il est nécessaire de lui fournir une référence de la cellule à sa création.
Il en est de même pour le tableau de cellules.
Pour que le comportement puisse analyser les cellules voisines, il faut qu'il ait un accès au tableau et à ses dimensions.
Voici le code correspondant au comportement du sable.
void SandMovement::update()
{
_target = nullptr; // Cell pointer
_x = _cell->getPosition().x;
_y = _cell->getPosition().y;
if (_y < _cell->getHeight() - 1) // Don't check out of arrays bounds
{
checkBelowCell();
if (targetFound() == false)
{
_random = (rand() % 2) * 2 - 1; // Randomly generate +1 or -1
checkAdjacentBelowCells();
}
if (targetFound() == true)
_cell->swapCell(*_target);
}
}
La première étape sert à récupérer la position de la cellule actuelle mais également à initialiser la cellule "cible" comme non-trouvée.
Après avoir vérifié que la cellule ne soit pas déjà tout en bas de la grille, le comportement vérifie si la cellule juste en dessous peut servir de cible.
Si ce n'est pas le cas, il vérifie ensuite les cellules en bas à droite et gauche (dans un ordre aléatoire).
Enfin, si une des cellules scrutée remplie toutes les conditions, celle-ci sera intervertie avec la cellule actuelle.
Voici la définition des méthodes utilisées par le code précédent.
void SandMovement::checkBelowCell()
{
if (_cells[_y + 1][_x].getType() < CellType::Solid)
_target = &(_cells[_y + 1][_x]);
}
void SandMovement::checkAdjacentBelowCells()
{
int x1 = _x + _random;
int x2 = _x - _random;
if (x1 >= 0 && x < _cell->getWidth() && _cells[_y + 1][x1].getType() < CellType::Solid)
_target = &(_cells[_y + 1][x1]);
else if (x2 >= 0 && x2 < _cell->getWidth() && _cells[_y + 1][x2].getType() < CellType::Solid)
_target = &(_cells[_y + 1][x2]);
}
const bool SandMovement::targetFound()
{
return _target != nullptr;
}
Pour qu'une cellule soit une cible valide, il faut que son type soit "inférieur" à celui de la cellule actuelle, autrement dit, inférieur au type "solide".
C'est l'utilisation des énumérations de C++ qui rend l'opération inférieur possible.
La première valeur a avoir été déclarée dans l'énumération est l'état "gazeux", cette valeur est donc associée à la valeur numérique zéro.
Suivant le même principe, l'état "liquide" est associée à un et l'état "solide" à deux.
Au lancement de l'application, toutes les cellules seront par défaut de type "gazeuse" et auront un mouvement les rendant statiques.
Voici une démonstration du comportement de mouvement implémenté.
Le sable possède le comportement attendu mais il y a quelque chose de surprenant dans cette vidéo.
Impossible de le voir tomber, dès que celui-ci est placé, il tombe instantanément au sol.
Actualiser les cellules
Ce problème vient de la manière dont les cellules sont actualisée.
Actuellement, pour chaque actualisation le programme va parcourir toutes les cellules et déclencher leur méthode update.
Pour parcourir les cellules, le programme commence par la position (0, 0) qui est en haut à gauche et va se diriger vers la fin de la ligne avant de passer à la suivante.
Cependant si une cellule se déplace, elle risque de se faire actualiser plus d'une fois par le programme.
Il y a plusieurs solutions pour pallier à ce soucis
La première consiste à mettre à jour les cellules en commençant par le bas.
Impossible pour les cellules qui tombent de se faire mettre à jour plusieurs fois.
En revanche le problème sera le même pour des types de mouvements faisant aller les cellules vers le haut.
Une deuxième solution serait de ne pas effectuer de changement sur le tableau en cours avant d'avoir mis à jour toutes les cellules. Cette technique requiert un second tableau, (doublant la taille de notre programme à son éxécution). De plus, il y a des risques de conflits dans le cas où deux cellules devraient se déplacer au meme endroit.
La dernière possibilité consiste à vérifier si la cellule à déjà été actualisée et de continuer à itérer sur le tableau,
tant que toutes les cellules n'ont pas été mises à jour.
Loin d'être la plus optimisée l'avantage de cette technique est sa simplicité de mise en place.
Il suffit de rajouter un indicateur (une valeur booléenne) aux cellules qui est vérifiée avant de mettre à jour la cellule.
Une fois toutes les cellules actualisées, leur indicateur est remis à zéro.
Le résultat est bien mieux que précédemment.
Il y a cependant un comportement étrange lorsque le sable est remplacé par du vide.
Le sable plus en hauteur s'affaisse toujours du même côté.
A savoir le côté gauche.
Le problème vient encore une fois de la manière dont sont mises à jour les cellules.
Malgré le fait qu'il n'y ait plus de multiples actualisation pour une même cellule, le programme actualise toujours les cellules de gauche à droite.
Ainsi, pour obtenir un résultat un peu plus chaotique, il faut actualiser toutes les cellules de la même ligne dans un ordre aléatoire.
Plutôt que de générer une séquence aléatoire à chaque mise à jour de l'application (ce qui serait très couteux), il est possible d'en créer une multitude au lancement du programme, et d'alterner entre ces différentes séquences à chaque mise à jour.
Chaque séquence sera contenue dand un tableau dynamique (vecteur de C++) et toutes les séquences seront stockées dans un tableau.
Voici le code pour générer un nombre N de séquences contenant des nombres allant de 0 à la largeur de la grille.
void Application::generateRandomSets(const int& N)
{
_randomSets = new std::vector[N];
for (int i = 0; i < N; i++) // For each set
for (int j = 0; j < CELL_WIDTH; j++) // Fill with numbers from 0 to CELL_WIDTH
_randomSets[i].push_back(j);
// Shuffle numbers in sets
auto rng = std::default_random_engine {};
for (int i = 0; i < N; i++)
std::shuffle(_randomSets[i].begin(), _randomSets[i].end(), rng);
}
Cette méthode va d'abord remplir tous les vecteurs avec les nombres dans l'ordre.
Puis avec l'usage de la librairie standard, elle va ensuite mélanger le contenu de chaque tableau dynamique afin d'avoir une multitude de séquences aléatoires.
Ainsi au lieu de parcourir les cellules de gauche à droite, il faut utiliser les nombres de la séquence actuelle en tant qu'indice.
Voici maintenant le morceau de code permettant de mettre à jour toutes les cellules.
size_t cellsUpdated = 0;
while (cellsUpdated < CELL_HEIGHT * CELL_WIDTH)
{
for (int y = 0; y < CELL_HEIGHT; y++)
{
for (int x = 0; x < CELL_WIDTH; x++)
{
// Retrieve x position from current set
int xPos = _randomSets[_currentRandomSet].at(x);
// If cell was not already updated
if (_cells[y][xPos].update())
cellsUpdated += 1;
}
// Update set
_currentRandomSet = (_currentRandomSet + 1) % RANDOM_SETS_NB;
}
}
Au lieu de prendre comme position la variablexallant de zéro à CELL_WIDTH,
on récupère la valeur stockée à l'indicex dans la séquence de nombres aléatoires.
Comme voulu, le résultat est plus chaotique, rendant le comportement du sable plus intéressant.
Jusqu'à présent il y a eu beaucoup de mise en place du "moteur".
Le résultat actuel n'est certes, pas le plus optimisé, néanmoins il est pleinement fonctionnel et ne subira plus de modifications majeures .
Le champ est maintenant libre pour se concentrer en profondeur sur les différents matériaux ainsi que leurs comportements.
Créer différents comportements
Pour créer le premier liquide, quoi de mieux que de commencer par l'eau.
Il est important de rappeler ici que le but n'est pas de reproduire le plus fidèlement possible des comportements mais de les simuler de manière simple et amusante.
Autrement, à lui seul, le domaine de la dynamique des fluides aurait pu être un projet.
Les mouvements de l'eau reprennent ceux du sable.
On souhaite qu'elle puisse subir la gravité et couler en pente.
Cependant, elle doit en plus former une surface plane lorsqu'elle à fini de s'écouler.
Ansi, en plus de pouvoir de se déplacer vers les trois cellules sous elle, elle doit être capable de bouger sur les cellules à sa gauche et à sa droite.
L'ordre dans lequel sont testés ses déplacements reprend celui du sable avec à la fin le nouveau test des déplacements horizontaux.
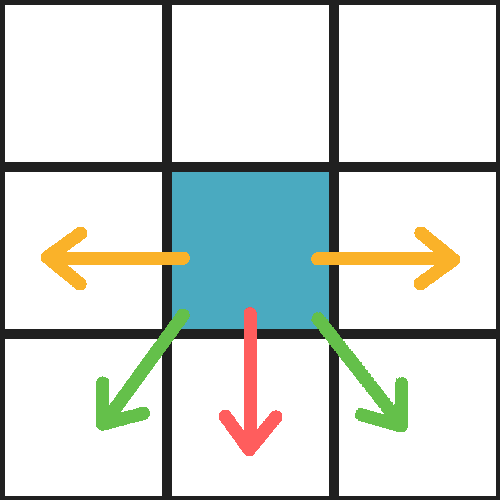
void WaterMovement::update()
{
_target = nullptr; // Cell pointer
_x = _cell->getPosition().x;
_y = _cell->getPosition().y;
if (_y < _cell->getHeight() - 1) // Don't check out of arrays bounds
{
checkBelowCell();
_random = (rand() % 2) * 2 - 1; // Randomly generate +1 or -1
if (targetFound() == false)
checkAdjacentBelowCells();
}
if (targetFound() == false)
checkAdjacentCells();
if (targetFound() == true)
_cell->swapCell(*_target);
}
Le code est très similaire à celui des mouvements du sable vu précémment, si ce n'est pour l'appel de la nouvelle méthodecheckAdjacentCells.
void WaterMovement::checkAdjacentCells()
{
int x1 = _x + _random;
int x2 = _x - _random;
if (x1 >= 0 && x < _cell->getWidth() && _cells[_y][x1].getType() < CellType::Liquid)
_target = &(_cells[_y][x1]);
else if (x2 >= 0 && x2 < _cell->getWidth() && _cells[_y][x2].getType() < CellType::Liquid)
_target = &(_cells[_y][x2]);
}
Afin d'éviter de dupliquer du code, il est possible de créer plusieurs fonctions appartenants à l'interfaceIMovementBehavior.
Ces fonctions pourront ainsi être réutilisée par toutes les classes qui vont hériter de l'interface.
Voici une vidéo du résultat avec l'eau conçue telle que décrite ci-dessus.
L'eau tend bien vers un niveau plat, cependant elle met beaucoup de temps à s'étaler.
La simple utilisation d'une boucle permet d'implémenter cette idée.
Pour ne pas traverser de cellules, il est important de sortir de la boucle (instruction
On constate sur la vidéo ci-dessous qu'une différence est notable, d'une part à cause le vitesse d'écoulement,
mais également à l'aide de ces petites "éclaboussures" qui apparaissent quand l'eau est en train de s'équilibrer.
Le comportement de l'eau commence à devenir complet et intéressant, en revanche, celui du sable paraît un peu plus léger.
Une première application de vélocité serait pendant la chute d'une cellule.
En chute libre, une cellule accumulerait une certaine vitesse et la dépenserait à l'impacte.
Plus concrètement, la vitesse d'une cellule va impacter son comportement lors de la recherche d'un possible mouvement.
A chaque unité de vélocité supplémentaire, la distance de vérification augmentera de un.
La prochaine vidéo présente les effets du code montré.
Le sable prend bien de la vitesse en chute libre et se fait bel et bien ralentir par l'eau lorsqu'il entre en collision avec.
Il est possible de transmettre sa vitesse aux cellules voisines à l'impacte.
C'est d'ailleurs ce qui a été brièvement fait (sans franc succès) dans l'application finale, cependant ce sujet ne sera pas couvert sur cette page.
La vitesse accumulée pendant la chute, va permettre à la cellule de rebondir plus ou moins haut une fois en collision avec le sol.
La première partie est plutôt simple.
Si une cellule ne peut plus se déplacer (autrement dit, si elle ne trouve pas de cible), et qu'elle possède encore de la vitesse.
Cela veut dire que la cellule vient d'entrer en collision avec le sol.
Pour libérer la vitesse accumulée, la cellule va temporairement adopter un nouveau comportement.
Ce principe permet de ne plus considérer le comportement initial de la cellule, le temps que celle-ci dépense son énergie.
Cela évite que la cellule cherche à aller vers le bas (pour le sable) quand on souhaite qu'elle se déplace vers le haut à cause d'un rebond.
Voici comment créer une particule, ainsi qu'une partie du code de déplacements des particules.
Les méthodes de déplacements, appelées dans
La dernière méthode utilisée,
Pour mieux visualiser les cellules possédant de la vélocité, il est possible de créer un filtre mettant en évidence ces cellules.
Pour uniquement visualiser les cellules avec de la vitesse, il serait possible d'uniquement afficher en couleurs ces cellules et de peindre les autres en une couleur unie.
Cependant, comme la vidéo le montre, il est difficile de comprendre ce qui ce passe dans la simulation.
Pour rendre ce qui se passe à l'écran plus compréhensible, il est possible de convertir la couleur RGB des cellules en nuances de gris.
Il existe plusieurs formules, voici celle utilisée ici.
Il serait même possible de changer la couleur en fonction de la direction et/ou de la rapidité de la cellule.
Les comportements de mouvements sont désormais visualisables et fonctionnels.
La structure du projet et la manière dont les cellules ont été conçues permettent à celle-ci de posséder plusieurs types de comportement.
Ces nouveaux comportements permettent de simuler la température des cellules et donc le changement d'état de certains matériaux.
La seule condition technique (personnellement imposée) à respecter, est de ne pas "générer" ou "supprimer" de chaleur.
En ce qui concerne l'impémentation de ces comportements thermiques, ils seront très similaires à ceux de mouvements.
Les cellules possèderont toutes un comportement thermique qui sera mis à jour dans leur méthode
Dans le but de faire une fonction permettant de propager la température des cellules.
L'idée la plus simple consiste à faire pour chaque cellule une moyenne de sa température et de celle de ses voisines.
Initialement dans la simulation toutes les cellules sont à une température de vingt degrés Celsius et le sable est à cinquante degrés quand il est créé.
Il est notable que la chaleur du sable créé se propage, en revanche la température moyenne affichée ne cesse de changer, même lorsqu'aucune cellule n'est ajoutée.
Une approche plus "réaliste", serait de considérer la chaleur comme une ressource, et que celle-ci cherche à s'équilibrer.
Ainsi, si deux cellules sont voisines et qu'elles n'ont pas la même température, la cellule avec le plus de chaleur va transmettre une partie de sa température à l'autre.
La fonction
Dans la simulation, la cellule échange cinq pourcent de sa température avec son voisin.
En relancant la simulation avec cette nouvelle méthode, on constate que cette fois-ci, la température moyenne est stable et ne change qu'à l'ajout de nouvelles cellules.
La solution est de garder en mémoire cette "nouvelle température" pour chaque cellule, et de l'appliquer une fois toutes les cellules mises à jour.
Pour augmenter le réalisme de la simulation, il est possible de rajouter un coefficient à chaque cellule pour favoriser ou non, les échanges de température.
Il est maintenant possible de créer différents comportements thermiques qui feront changer les caractéristiques des cellules en fonction de leur température.
Voici le code permettant à l'eau de changer d'état en fonction de sa temperature.
Il est à partir de maintenant possible de créer toutes sortes d'éléments et de jouer avec leur température pour créer de multiples réactions.
Ce projet a été extrêmement fun et divertissant.
Il est bien sûr possible d'aller encore plus loin mais je suis satisfait de ce qui a été fait et compte m'arrêter là.
Il est très plaisant de partir d'une base simple et de petit à petit, compléxifier le tout sans aucune limite.
Quand à l'amélioration de ce qui existe déjà, il serait plus efficace d'utiliser une texture pour l'affichage de la grille au lieu d'afficher chaque cellule individuellement.
Dan-Ball | Powder Game 2 : https://dan-ball.jp/en/javagame/dust2/
Une solution assez simple pour accélérer ce phénomène consiste à vérifier ses possibilités de déplacements horizontaux sur plusieurs cellules.
Dans le code suivant, l'eau ira chercher à se déplacer horizontalement sur cinq cellules.
void WaterMovement::checkAdjacentCells()
{
const int CHECK_LENGTH = 5;
for (int i = 1; i < CHECK_LENGTH; i++)
{
int x1 = _x + i * _random;
if (x1 >= 0 && x < _cell->getWidth() && _cells[_y][x1].getType() < CellType::Liquid)
_target = &(_cells[_y][x1]);
else
break;
}
if (targetFound())
return;
for (int i = 1; i < CHECK_LENGTH; i++)
{
int x2 = _x - i * _random;
if (x2 >= 0 && x2 < _cell->getWidth() && _cells[_y][x2].getType() < CellType::Liquid)
_target = &(_cells[_y][x2]);
else
break;
}
}
breakdans le programme)
dès qu'une cellule ne remplie pas les conditions pour être une cible.
Pourquoi ne pas essayer de le compléter en ajoutant un semblant de vitesse ?
Pour symboliser une vitesse, il est nécessaire de rajouter une caractéristique aux cellules.
Le choix a été de fait prendre un vecteur en deux dimensions (provenant de la librairie mathématiques GLM).
L'utilisation d'un vecteur en deux dimensions permet de représenter la vitesse et la direction en même temps.
La composante x du vecteur sera utilisée pour la vitesse sur l'axe horizontal et y, pour l'axe vertical.
Un vecteur de valeur x: 1 et y: -1 signifie que la cellule se dirigera vers la droite et également vers le haut (car la coordonnée 0, 0 du tableau se trouve en haut à gauche de l'écran).
L'usage de vitesse négative signifie donc que la cellule se déplace dans le sens contraire de l'axe.
A la manière dont l'eau cherchait à se déplacer horizontalement sur cinq cellules, le sable va chercher à se déplacer sur plusieurs cellules sous lui.
Cependant, la distance de recherche sera determinée par sa vitesse verticale.
void SandMovement::checkBelowCell()
{
for (int i = 0; i < _cell->getVelocity().y; i++)
{
if (_y + 1 + i < _cell->getHeight() && _cells[_y + 1 + i][_x].getType() < CellType::Solid)
_target = &(_cells[_y + 1 + i][_x]);
else
break;
}
}
Dans la méthodeupdatese trouve une nouvelle méthode, udpateVelocityayant pour rôle de modifier la vitesse
de la cellule actuelle, dépendant du type de la cellule avec laquelle celle-ci va changer de place.
Dans l'exemple suivant, la vitesse de chaque cellule va augmenter de 0.2 unité en chute libre mais va en perdre 0.8 en coulant dans un liquide.
void SandMovement::update()
{
// ... (previous code did not change)
if (targetFound() == true)
{
updateVelocity();
_cell->swapCell(*_target);
}
}
}
void SandMovement::updateVelocity()
{
if (_target->getType() == CellType::Gazeous) // Accelerate in free falling
_cell->setVelocity(_cell->getVelocity() + glm::vec2(0.0f, 0.20f));
else if (_target->getType() == CellType::Liquid && _cell->getVelocity().y >= 0.80f) // Get slow down by liquid
_cell->setVelocity(_cell->getVelocity() + glm::vec2(0.0f, -0.80f));
}
La question qui se pose alors, est, que faire de la vitesse accumulée, une fois que la cellule est au sol ?
La réponse va alors dépendre de jusqu'où veut-on pousser la simulation.
Pour ce faire, il faut premièrement identifier quand la cellule entre en collision avec le sol.
Puis trouver un moyen de convertir la vitesse accumulée en un "nouveau saut".
Ce qui peut se traduire par le code suivant.
void SandMovement::update()
{
// ... (previous code did not change)
if (targetFound() == true)
{
updateVelocity();
_cell->swapCell(*_target);
}
}
if (targetFound() == false && cellHasVelocity() == true)
{
// Release velocity
}
}
const bool SandMovement::cellHasVelocity() const
{
_cell->getVelocity() != glm::vec2(0.0f, 0.0f);
}
Ce nouveau comportement à pour but de faire déplacer la cellule en fonction de sa vitesse, et ce, qu'elle que soit son type.
Il faut donc que ce nouveau comportement garde en mémoire toutes les informations de la cellule, est les restituent, une fois que la vitesse accumulée est dépensée.
void SandMovement::update()
{
// ... (previous code did not change)
if (targetFound() == false && cellHasVelocity() == true)
_cell->setMovementBehavior(new ParticleMovement(_cell, *this));
}
void ParticleMovement::update()
{
if (_cell->getVelocity().y > 0.0f)
moveUpward();
else
moveDownward();
if (_cell->getVelocity().x > 0.0f)
moveLeft();
else
moveRight();
if (cellHasVelocity() == false)
setOriginalBehavior();
}
void ParticleMovement::setOriginalBehavior()
{
_cell->setMovementBehavior(&_originBehavior);
_cell->getMovementBehavior()->setCell(_cell);
delete this;
}
ParticleMovement::updatepermettent à la cellule d'échanger sa position avec ses cellules voisines tout en diminuant sa vitesse.
Celles-ci ne sont ni compliquées ni intéressantes, et ne sont donc pas présentées sur cette page.
Il est néanmoins possible d'utiliser d'autre méthodes, comme l'algorithme de tracé de segment de Bresenham
ou une fonction d'interpolation linéaire sphérique pour avoir un meilleur effet de déplacement des particules.
setOriginalBehaviorpermet de restituer le comportement d'origine à la cellule.
Comme celle-ci s'est déplacée sur la carte, il est important de donner au comportement la nouvelle position de la cellule (ligne 2 de la méthode).
Jusqu'à présent, les couleurs de la grille étaient dépendants de la couleur des cellules.
Cependant, il est possible d'afficher des couleurs en fonction de certaines propriétées des cellules.
void GridRenderer::updateColorFromVelocity(Cell** cells)
{
const glm::vec3 VELOCITY(1.0f, 1.0f, 1.0f) // White
const glm::vec3 NO_VELOCITY(0.0f, 0.0f, 0.0f) // Black
for (int y = 0; y < CELL_HEIGHT; y++)
{
for (int x = 0; x < CELL_WIDTH; x++)
{
glm::vec3 color;
// Set color to white if velocity not null
if (cells[y][x].getVelocity() == glm::vec2(0.0f, 0.0f)
color = NO_VELOCITY;
else
color = VELOCITY;
// Apply color to vertices
_vertices[vertexNb * 4].Color = color;
_vertices[vertexNb * 4 + 1].Color = color;
_vertices[vertexNb * 4 + 2].Color = color;
_vertices[vertexNb * 4 + 3].Color = color;
}
}
}
glm::vec3 rgbToGrayscale(glm::vec3 color)
{
float value = 0.0f;
value += color.r * 0.3f;
value += color.g * 0.59f;
value += color.b * 0.11f;
return glm::vec3(value, value, value);
}
Les éléments tel que la roche, la fumée ou encore l'acier, présents dans l'application finale, ne seront pas présentés en détails comme il a été fait avec le sable ou l'eau.
La base est identique et leurs implémentation est consultable dans le code source.
Les précédents comportements permettaient aux cellules de se déplacer, mais il est possible de créer une nouvelle dimension au projet
en rajoutant de nouveaux comportements de type thermique.
L'eau deviendra par exemple solide sous une basse température, et à l'inverse, sera dans état gazeux à température élevée.
Autrement dit, la simulation doit être similaire à une boite fermée et parfaitement isolée.
Tant qu'aucun changement n'est fait pendant l'exécution du programme, la température moyenne doit rester la même.
La seule raison pour laquelle la température moyenne doit pouvoir changer est car l'utilisateur est en train d'ajouter ou supprimer des éléments
update.
Ces comportements se baseront eux aussi sur une interface fournissant les fonctionnalitées de base comme la propagation de température.
Cette méthode devra être appelée au début de la fonctionupdatede chaque comportement thermique.
Il est en revanche possible de faire en sorte que ce soit fait automatiquement, c'est une amélioration potentielle du projet.
Le code ne sera pas détaillé car il est relativement simple et peu intéressant.
Pour mieux visualiser les échanges de température, un filtre a été mis en place pour afficher en couleur les cellules en fonction de leur température.
Le problème vient en majeure partie de la méthode utilisée pour les échanges de température.
Ce comportement ne créé ou ne supprime donc pas de chaleur, étant donné que les échanges dépendent de la température des cellules.
updateTargetest appliquée à chaque voisin de chaque cellule.
void IThermicBehavior::update(Cell& neighbor)
{
if (neighbor.getTemperature() >= _cell->getTemperature())
return;
const float TEMPERATURE_EXCHANGE_COEFF = 0.05f; // Transfer 5% of cell temperature
double temperatureExchanged = (_cell->getTemperature() - neighbor.getTemperature()) * TEMPERATURE_EXCHANGE_COEFF;
temperatureExchanged = fabs(temperatureExchanged);
float newNeighborTemperature = neighbor.getTemperature() + temperatureExchanged;
neighbor.setTemperature(newNeighborTemperature);
float newCellTemperature = _cell.getTemperature() - temperatureExchanged;
_cell->setTemperature(newCellTemperature);
}
Il est important de garder ce pourcentage inférieur à douze virgule cinq (résultat provenant de cent divisé par huit).
Car dans le cas où une cellule doit échanger sa température avec tous ses voisins,
elle pourrait donner plus de température qu'elle n'en possède si ce pourcentage est trop élevé.
La température de chaque cellule deviendrait alors instable et ne cesserait d'alterner entre valeur positive et négative avant
de dépasser la capacité de stockage d'un nombre à virgule, causant le crash de l'application.
Un dernier problème subsiste cependant. Une partie de la chaleur descend instantanément au plus bas de la grille, avant même que la cellule ne soit tombée.
Ce soucis est similaire à celui du sable qui était mis à jour plusieurs fois par image.
Ici, la température des cellules est calculée puis appliquée, dès que la cellule éxécute sa méthodeupdate.
Or, il est nécessaire que la température soit appliquée une fois que toutes les cellules ont été actualisées.
Ainsi, la méthodeupdatede IThermicBehavior ne modifie plus directement la température des cellules, mais plutot une nouvelle variable nommée "nextTemperature".
Le changement de température se fera sur toutes les cellules entre leurs mises à jours.
Un bon exemple est celui de l'eau.
A plus de cent degrés, l'eau doit devenir de la vapeur et en dessous de zéro, elle doit devenir de la glace.
Dans la méthodeupdatede la classe du comportement thermique de l'eau (qui hérite de IThermicBehavior).
Il faut premièrement mettre à jour la température et ensuite vérifier ces conditions.
Si la cellule doit change d'état, il faut modifier ses propriétés pour qu'elles correspondent au nouveau type de cellule voulu (glace, vapeur, ...).
Pour faire ces modifications, un objet contenant les caractéristiques initiales de tout les types de cellules nomméCellFactory va modifier la cellule voulue, pour la faire correspondre avec son nouveau type.
Dans le cas d'un passage de l'eau vers la glace, la cellule va changer de couleur ainsi que de comportement de déplacement.
void WaterThermic::update()
{
updateTemperature();
if (_cell->_temperature >= 100.0f)
CellFactory::configureSmokeCell(*_cell);
else if (_cell->_temperature <= 0.0f)
CellFactory::configureIceCell(*_cell);
}
Pour que la glace et la vapeur redeviennent de l'eau, il faut leur écrire un comportement similaire à celui-ci.
Voici un example de plusieurs éléments ajoutés en suivant les différents principes expliqués.
Conclusion
Pour ajouter de nouvelles dimensions à ce projet il serait possible d'implémenter l'élément "vide", une notion de luminosité, ou même diverses formes de vies.
Pour le comportement des cellules il doit être possible de les optimiser et de limiter le nombre d'allocations mémoires.
Et enfin, l'utilisation des threads permettrait au programme de mettre plusieurs groupes de cellules à jours simultanément ce qui augmenterait considérablement les performances.
Sources
Wikipedia | Falling-sand game : https://en.wikipedia.org/wiki/Falling-sand_game
Max Bittker | Making Sandspiel : https://maxbittker.com/making-sandspiel
MARF | How to code a falling sand simulation : https://www.youtube.com/watch?v=5Ka3tbbT-9E
John Jackson | Recreating Noita's sans simulation : https://www.youtube.com/watch?v=VLZjd_Y1gJ8
GDC | Exploring the Tech and Design of Noita : https://www.youtube.com/watch?v=prXuyMCgbTc
Téléchargement
